Lecture 3 - Indexing
# Indexes
# “Indexes will be our friends”
Main Indexes:
- B+ - Tree
- Hash Indexes
Example: The book has the table of contents - shoes topics in order (page numbe, you are advancing in the book sequencially); and the index at the end of the book (the page numbers is not order, in this case the index entries are sorted alfphabetically)
The ToC is a Clustered Index (ordered according the order of data)
The Index at the end is a non-Clustered Index (order)
Book Pages -> Disk Pages
# Ordered Indexes
# Dense Index
- Index record appears for every search-key value in the file dense_index.png)
Even without a pointer to some record, we can assume some “categories” are in between some other indexed categories
# Sparse Index
- Contains index records for only some search-key values
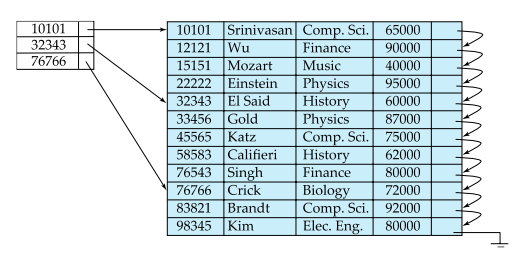
# Dense vs Sparse
Sparse compared to Dense Indexes:
- Less space and less maintenance overhead for insertions and deletions
- Generally slower than dense index for locating records
# Multilevel Index
- Problem: If index does not fit in memory, access becomes expensive
- Solution:
Treat index kept on disk as a sequential file and construct a sparse index on it
- Outer index – a sparse index of the basic index
- Inner index – the basic index file
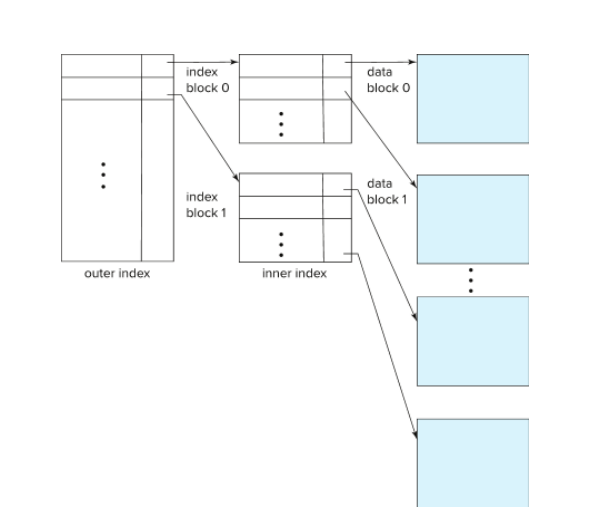
- Outer Indexes Sparse and inner Index Dense (for example).
- If even outer index is too large to fit in main memory, yet another level of index can be created, and so on.
- Allows us to jump directly to some part of the table
- Indexes at all levels must be updated on insertion or deletion from the file
# Clustered Index
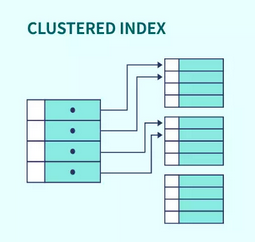
- In a sequentially ordered file, the index whose search key specifies the sequential order of the file
- Clustered Indexes sort and store the data rows in the table or view based on their key values.
- These are the columns included in the index definition.
- There can be only one clustered index per table, because the data rows themselves can be stored in only one order.
All records regarding to a column are sequencial, so its faster to retrieve them
If you have a pointer pointing to the first record in a table we only need that one, because the other ones follow it.
# Non-Clustered Index
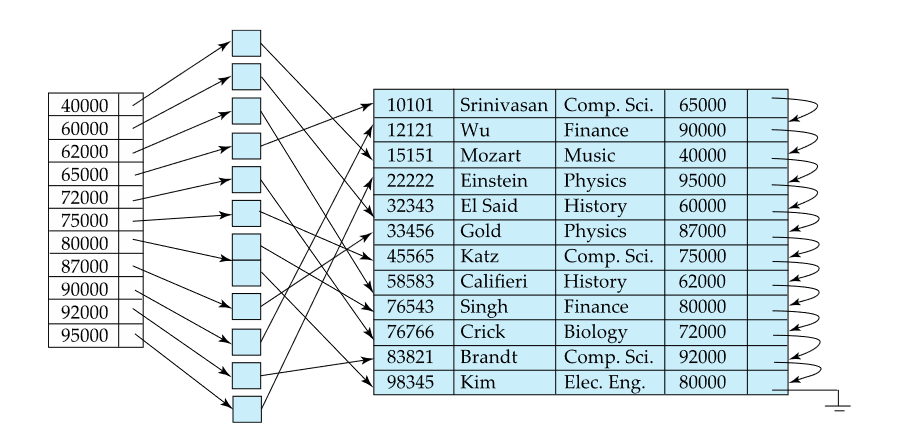
- There can be multiple non-clustered indexes on a table.
- Index record points to a bucket that contains pointers to all the actual records with that particular search-key value
- Different order from the data
- Must be dense
The pointer from an index row in a nonclustered index to a data row is called a row locator. The structure of the row locator depends on whether the data pages are stored in a heap or a clustered table. For a heap, a row locator is a pointer to the row. For a clustered table, the row locator is the clustered index key.
More info on clustered and non-clustered Indexes
# B+ -Tree
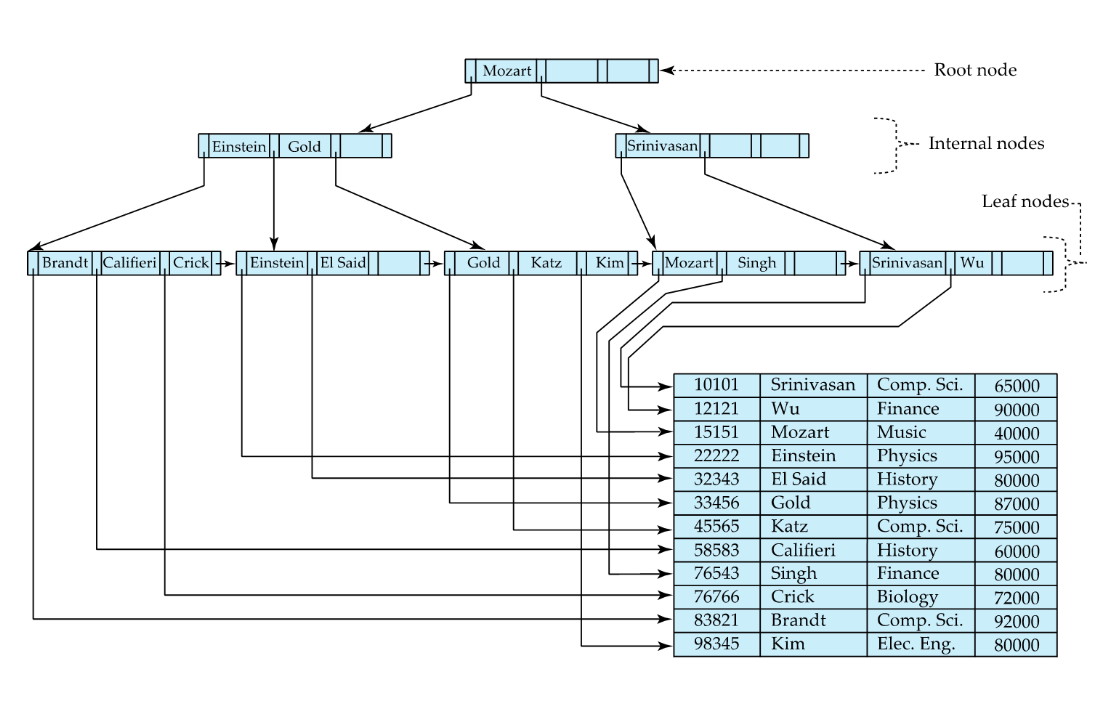
# Searching for “Katz”
- Decide if Katz comes before/after Mozart -> follows pointer to the left (K<M)
- Theres no Katz here (sparse index) -> follow pointer to the right (K>E && K<G)
- This is a dense index: If value is there -> follow pointer
# Properties
- We only read 1 record.
- if the table is large -> the dense index will be very large -> bad performance
- By having the other levels we can jump in bigger intervals
- The more entries grows the width exponentially (you iterate it in linear time), But it grows the height logarithmically (reverse exponential going up)
# B+ -Tree Insertion
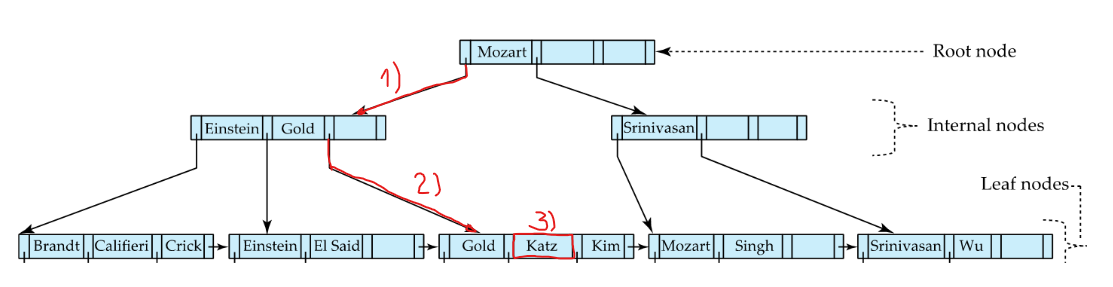
Inserting Adams:
Adams < Mozart Adams < Einstein Adams < Brandt
We need to put it in the front But Adams doesnt fit in the node
# Splitting Procedure
- Split node and split the values between the two (space increased from 3 to 6)
- 2 values in the first node and the other 2 in the other node
- We have space in the 2nd last level, we change the pointers by pushing them to the right
- To chose the new pointer values we assess the values in the leaf nodes (Califeri < Adams; Califeri < Brandt)
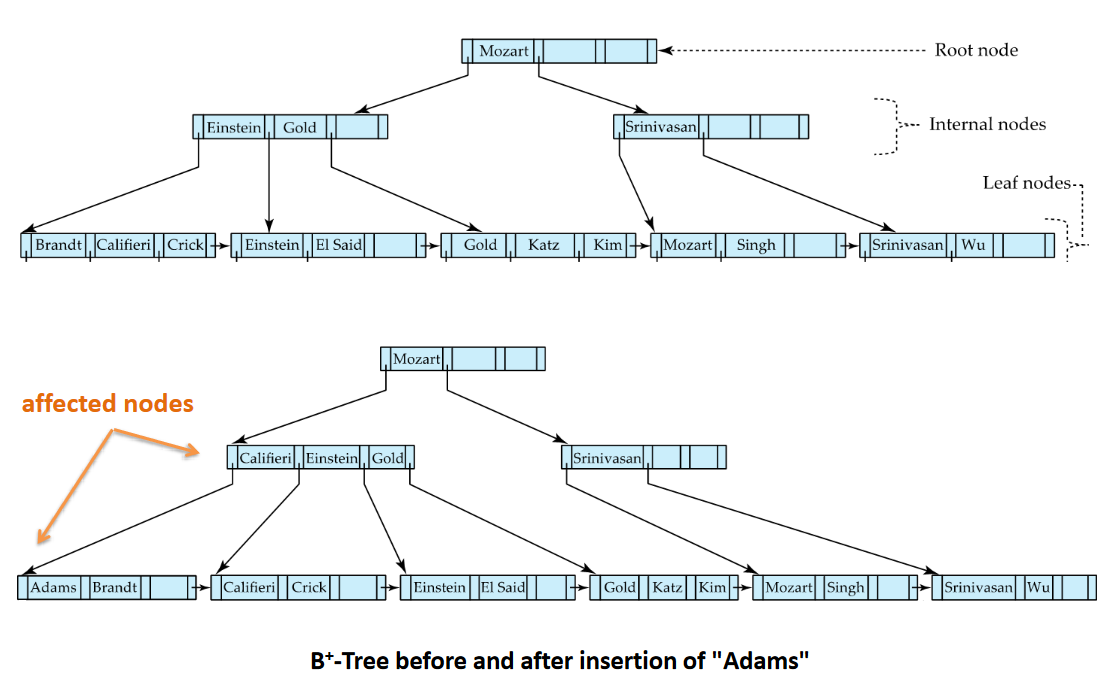
Inserting Lamport:
It should be in-between Kim and Mozart
Add more nodes -> need more pointers Problem: Previous level has no space Solution: Split nodes recursively
Add another level -> Add another leaf -> Choose adequate value in level for pointer -> Correct Root
Left has to have values < Right has to have values >=
The root value has to be the smallest value in the leaf section
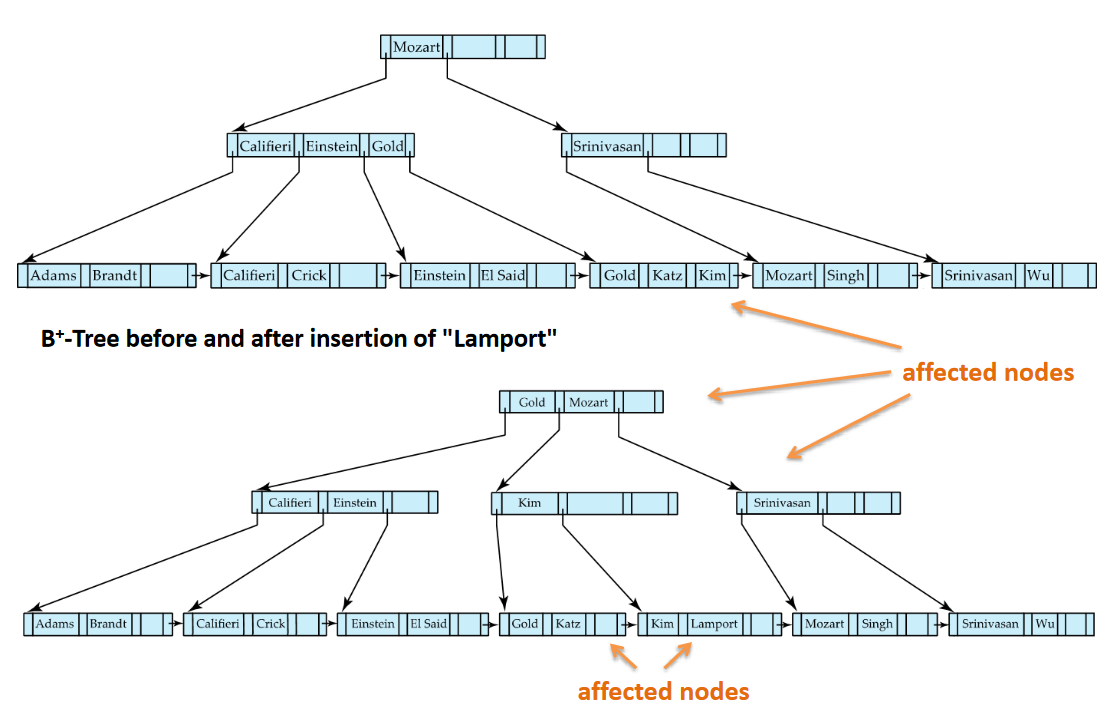
# Deleting Entries
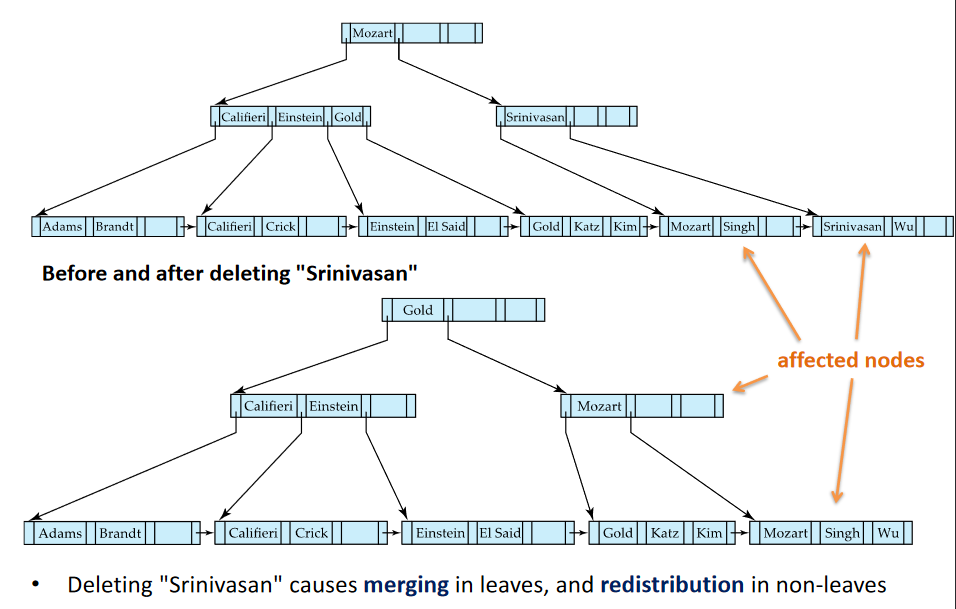
Merging and Redistribution Removing a Leaf, Srinivasan:
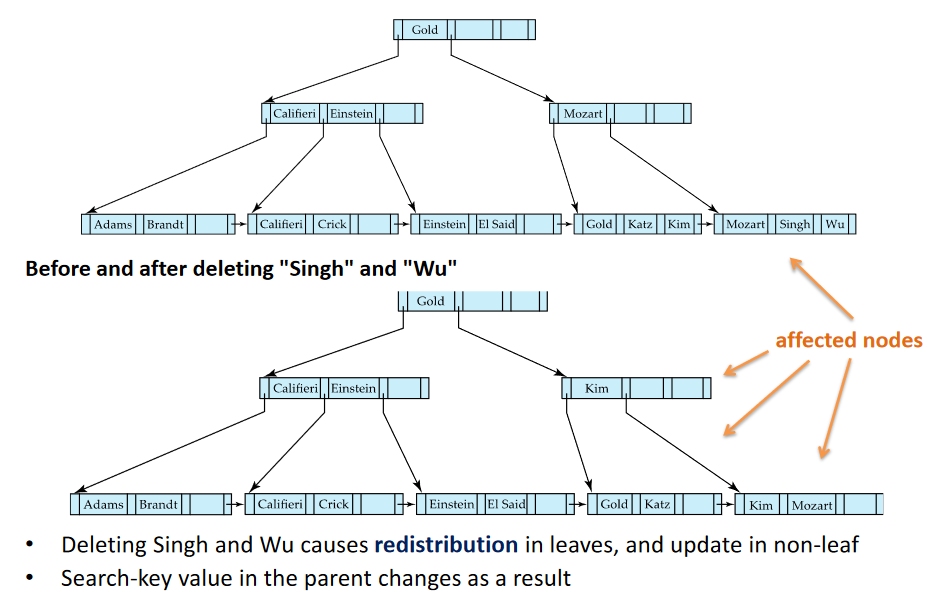
Removing 2 non-Leaves Singh and Wu:
Removing a root, Gold:
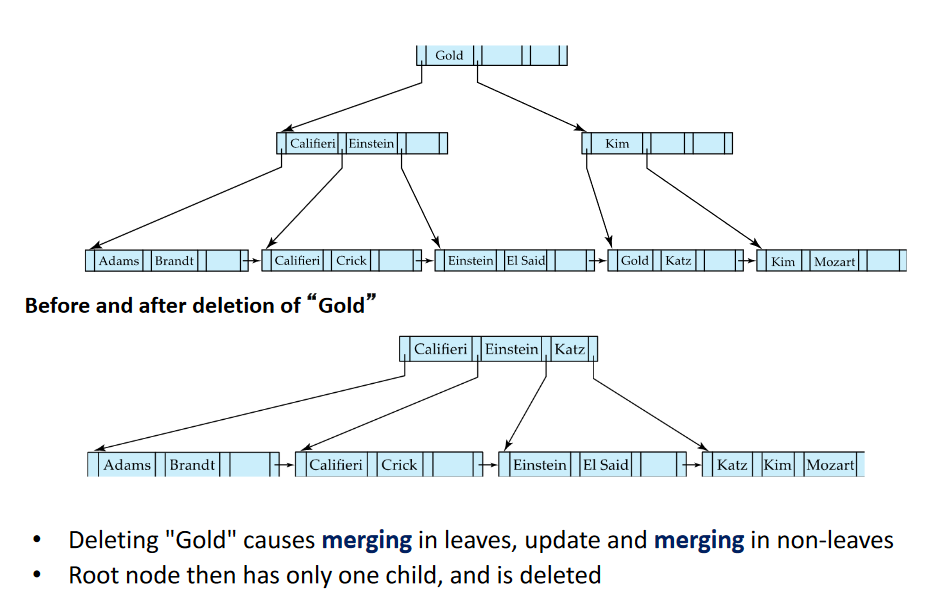
- Check where Gold is (at Root -> Less than Kim -> found leaf)
- No need for this many nodes -> Merge Nodes
- Causes the existing os a single Pointer -> Go get a new pointer (Left)
- No need for root -> Delete has it only has 1 child
- Assess pointer values
# Indexes Notes:
- Very nice to have, has it allows to jump to records
- Indexes are not free; Changing data is very costly. Trade-off between insertion/deletion and speed searching (imagine updating the Table of Contents of the book and adding entries to the Index ate the end of the books)
- Indexes are stored in memory (Disk) -> the nodes are the size a disk block; If the node is smaller than a block, then were reading empty space; if is bigger, we might be reading from different plaecs in the disk)
- You read the same number of blocks everytime an index is used. The search time is constant (B+-Tree); in a dense index you read 1->N
# Hash File organization
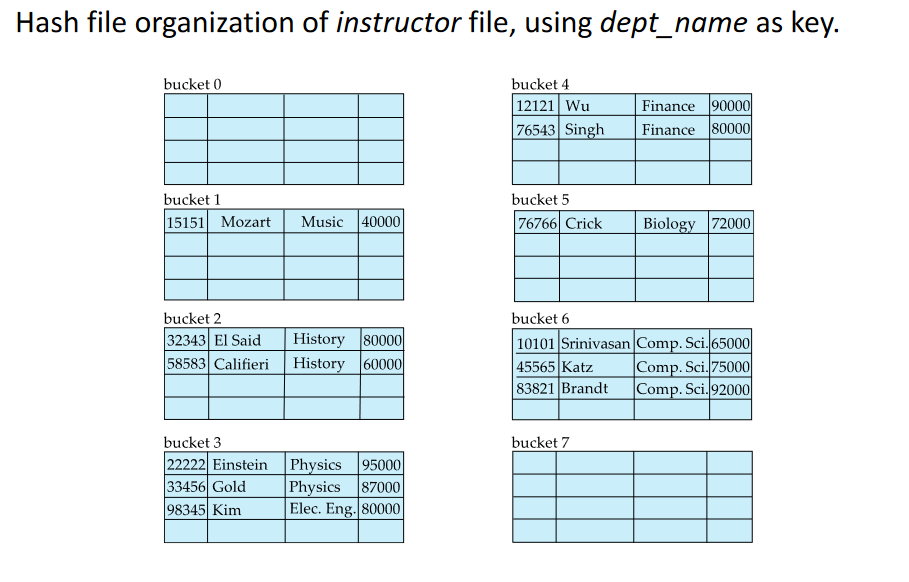
# Hash Indexes
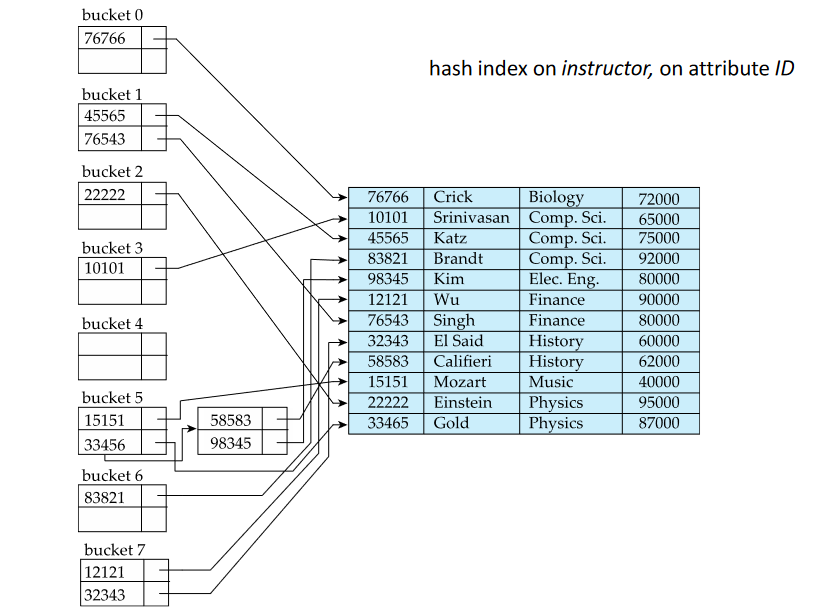
- In a hash index, buckets store entries with pointers to records
- In a hash file-organization buckets store records
Worst hash function maps all seach-keys to the same bucket An ideal hash function is uniform and random
Is organized in buckets or containers.
- We assign values to this cointainers based on a hash function.
- Apply hash function on a value and get a container
Problem:
Too many entries in a single bucket Causes Overflow Bucket It is a sign that the hash funciton is not well designed or we have too many entriesOne Solution: Create an Overflow Bucket that is being pointed at by an entry in another Bucket. This defeates the purpose of an Hash Index
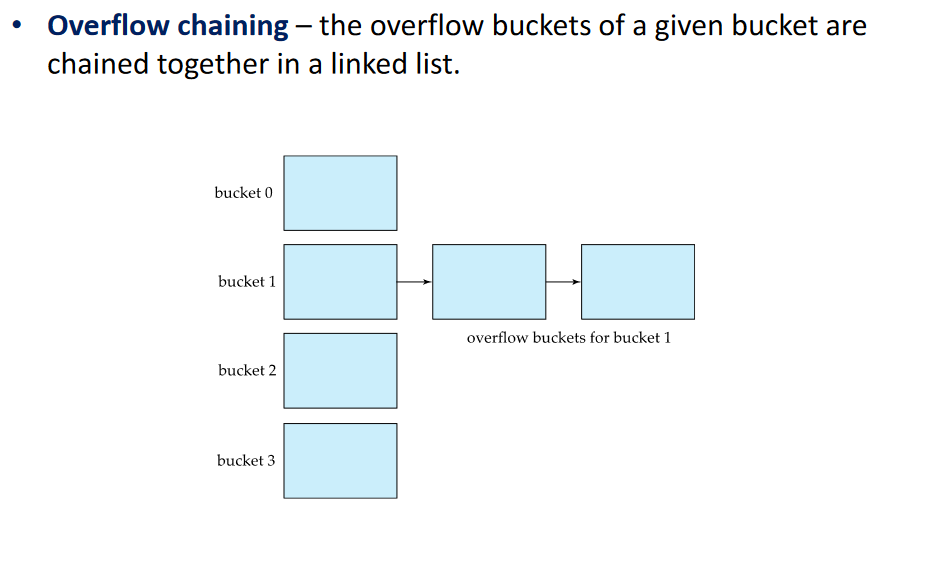
The same principle of B+-Tree index Node size applies to containers: A Bucket is the same size of a disk block.
As we grow the number of entries and therefore the number of bucket, we might need to change the hash function
# Static Hashing Deficiencies
In static hashing, function ℎ maps search-key values to a fixed set of 𝐵 of bucket addresses. Databases grow or shrink with time.
- If initial number of buckets is too small, and file grows, performance will degrade due to too much overflows.
- If space is allocated for anticipated growth, a significant amount of space will be wasted initially (and buckets will be underfull).
- If database shrinks, again space will be wasted.
One solution: periodic re-organization of the file with a new hash function
- Expensive, disrupts normal operations
Better solution:
- Allow the number of buckets to be modified dynamically
# Extendable Hash Structure
Context: We have a single bucket -> We have a hash function that with any value indicates that bucket
1-bit prefix
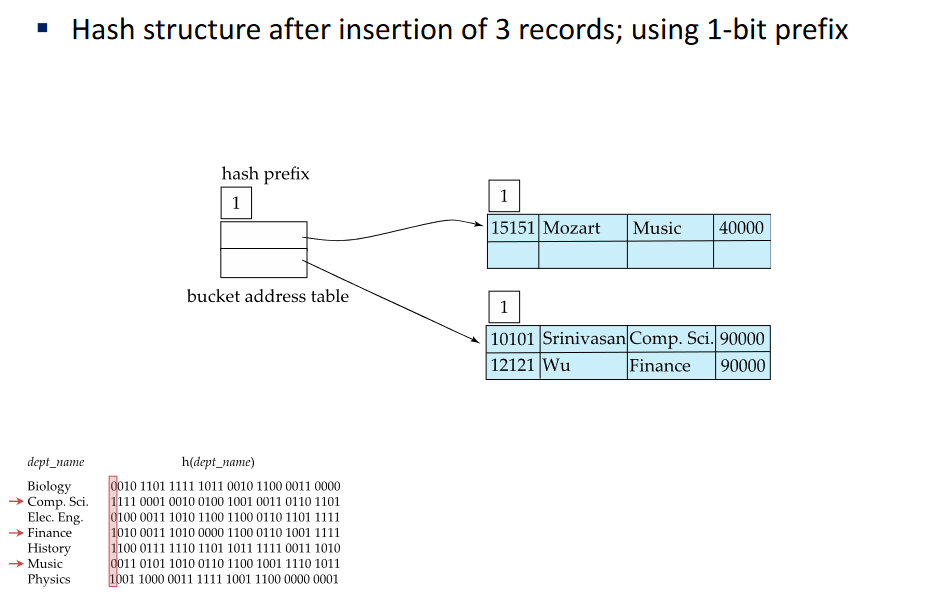
Suppose we consider the first bit from the value; Not all values fit into the bucket: 3 entries->2 values with 0’s are inserted but another one is not
Need more buckets… need more bits
2-bit prefix
00, 01, 10, 11
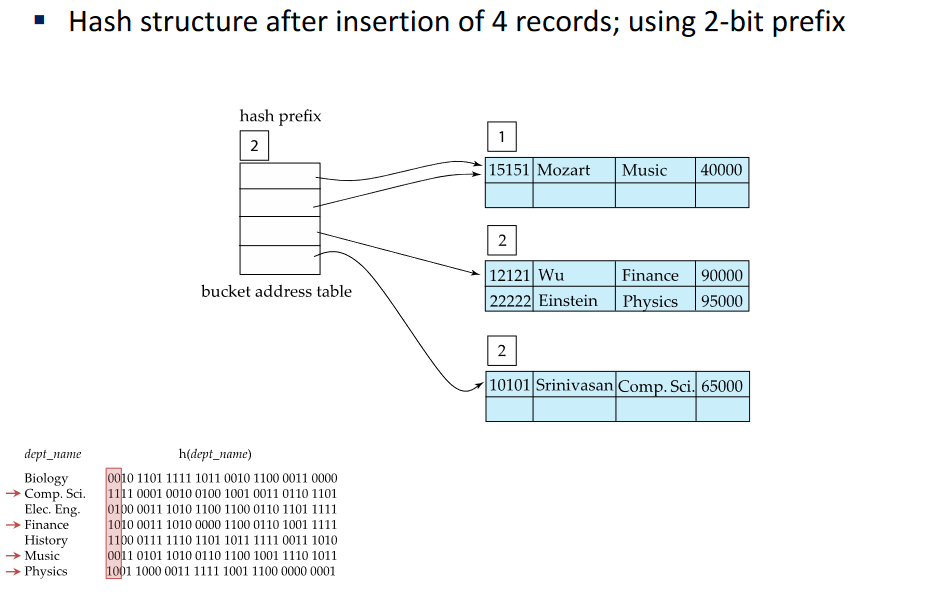
01 hash value is not being used -> using 1-bit prefix in the first bucket
3-bit prefix
last bucket: first 2 bits are 1 so this bucket is still 2 bit
we need 3 bits for some buckets (physics and finance)
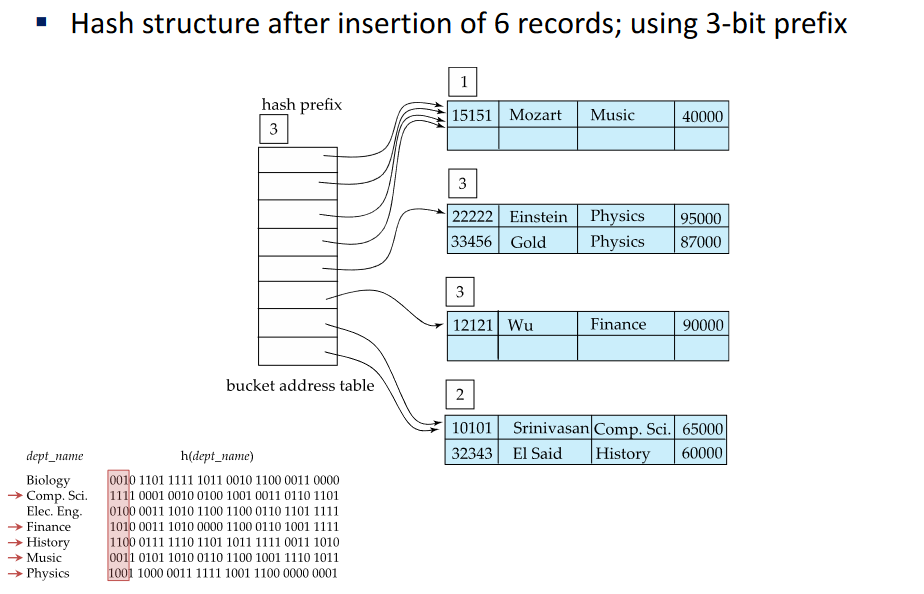
Now inserting another record and we dont have space, we just start to consider another bit in the bucket
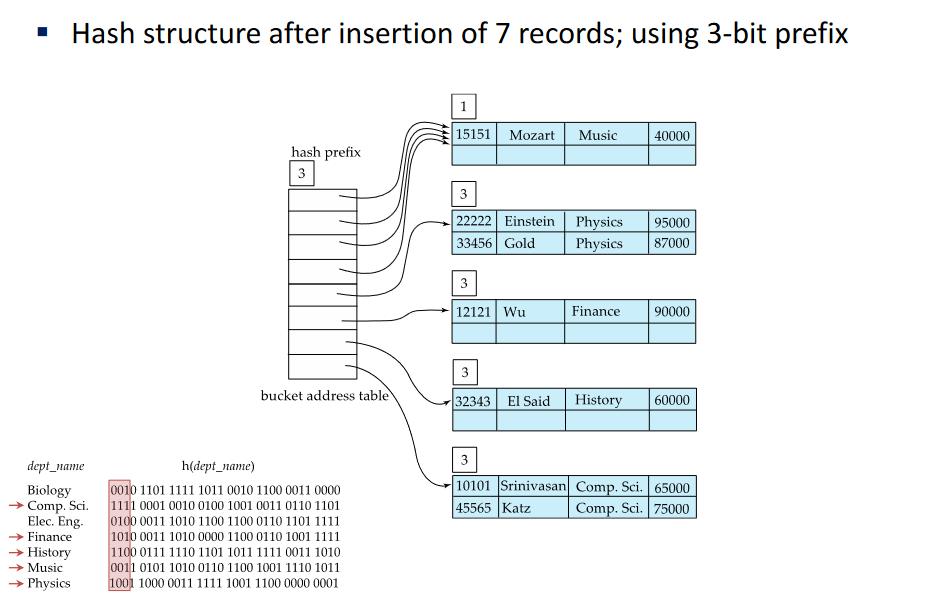
Once have buckets filled with the same value, overflow buckets are bound to happen, we dont need to consider anymore bits to those buckets
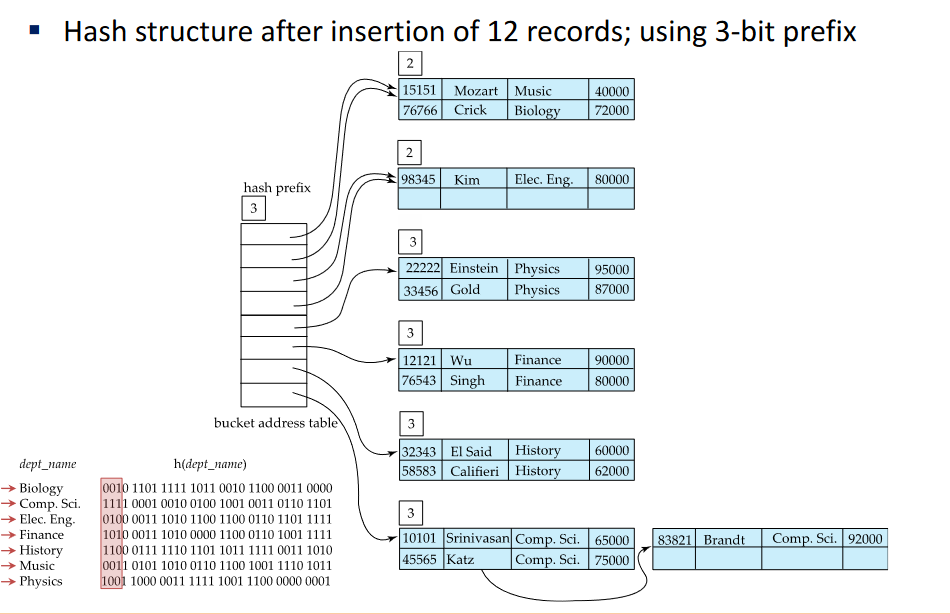
Collisions happens usually due to same value collision
Theres always 2 solution, consider more bits in a bucket or double the bucket address table (2x)
Using another bit in the prefix does not mean we use more buckets Pointers grow exponentially, buckets not
# General Extendable Hash Structure Use

# Hash Notes
- Hashing is generally better at retrieving records having a specified value of the key.
- If range queries are common, ordered indices are preferred
- In practice:
- PostgreSQL supports hash indices, but discourages its use
- Oracle supports static hash organization, but not hash indices
- SQLServer supports B+-trees; hash indexes in memory only
- Hash-indices are extensively used in-memory but not used much on disk
# Bitmap Index
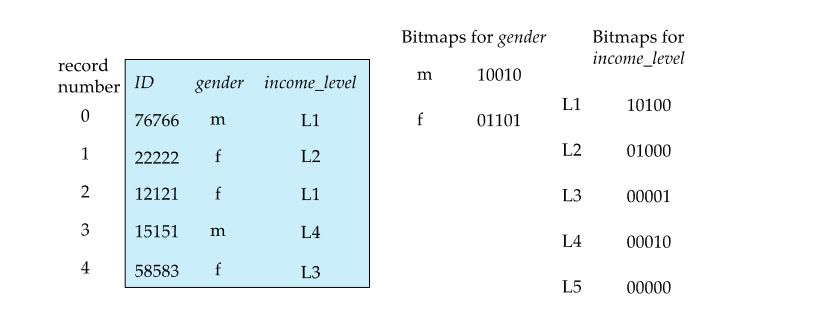
Bitmaps for gender: m/f = 1 for each reacord same for income_level
Use: “find all records for gender “f” and income_level “L3"” Do an AND operation and we get the last record
same for other operations
- usually we dont create the bitmaps (the dbms does it for certain queries as an optimization, you can see it in “Execution Plan”)
- easy to build, then is thrown away
Lecture 2 Storage and file organization | Lecture 4 Query Processing